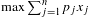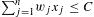| Article ID: | iaor20102990 |
| Volume: | 37 |
| Issue: | 5 |
| Start Page Number: | 303 |
| End Page Number: | 306 |
| Publication Date: | Sep 2009 |
| Journal: | Operations Research Letters |
| Authors: | Tamir Arie |
| Keywords: | knapsack problem |
We consider the bounded integer knapsack problem (BKP)