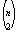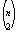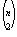Ancestor tree for arbitrary multi-terminal-cut functions

In many applications, a function is defined on the cuts of a network. In the max-flow min-cut theorem, the function on a cut is simply the sum of all capacities of edges across the cut, and what is wanted is the minimum value of a cut separating a given pair of nodes. To find the minimum cuts separating pairs of nodes, it only needs computations to construct the cut-tree. In general, arbitrary values associated with all cuts in a network can be defined, and assumed that there is a routine which gives the minimum cut separating a pair of nodes. To find the minimum cuts separating pairs of nodes, it also only needs n-1 routine calls to construct a binary tree which gives all minimum partitions. The binary tree is analogous to the cut-tree of Gomory and Hu.