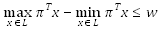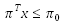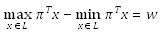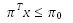| Article ID: | iaor20102618 |
| Volume: | 35 |
| Issue: | 1 |
| Start Page Number: | 233 |
| End Page Number: | 256 |
| Publication Date: | Feb 2010 |
| Journal: | Mathematics of Operations Research |
| Authors: | Weismantel Robert, Louveaux Quentin, Andersen Kent |
A maximal lattice free polyhedron