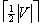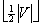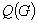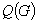| Article ID: | iaor19921039 |
| Country: | Netherlands |
| Volume: | 49 |
| Issue: | 1 |
| Start Page Number: | 49 |
| End Page Number: | 70 |
| Publication Date: | Nov 1990 |
| Journal: | Mathematical Programming |
| Authors: | Conforti Michele, Sassano Antonio, Rao M.R. |
| Keywords: | graphs, programming: integer, programming: quadratic |
The following basic clustering problem arises in different domains, ranging from physics, statistics and Boolean function minimization. Given a graph