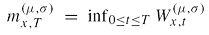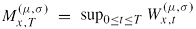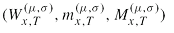We introduce a method for generating
 , where
, where
 denotes the final value of a Brownian motion starting in x with drift μ and volatility σ at some final time T,
denotes the final value of a Brownian motion starting in x with drift μ and volatility σ at some final time T,
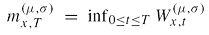 and
and
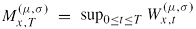 . By using the trivariate distribution of
. By using the trivariate distribution of
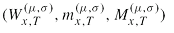 , we obtain a fast method which is unaffected by the well-known random walk approximation errors. The method is extended to jump-diffusion models. As sample applications we include Monte Carlo pricing methods for European double barrier knock-out calls with continuous reset conditions under both models. The proposed methods feature simple importance sampling techniques for variance reduction.
, we obtain a fast method which is unaffected by the well-known random walk approximation errors. The method is extended to jump-diffusion models. As sample applications we include Monte Carlo pricing methods for European double barrier knock-out calls with continuous reset conditions under both models. The proposed methods feature simple importance sampling techniques for variance reduction.