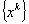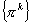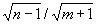A new variant of the primal affine scaling algorithm for linear programs

In this paper, a new variant of the primal affine scaling algorithm for linear programming problem is developed. The authors show that, under the assumptions of bounded feasible region and primal and dual nondegeneracy, the algorithm generates two sequences, and , of points that converge to the primal and the dual optimal solutions, respectively. Compared to the primal affine scaling algorithm proposed by Barnes, Cavalier-Soyster, and Vanderbei-Meketon-Freedman, the new algorithm shows a better asymptotic convergent rate. For a standard linear program with n variables and m constraints, the limiting convergent rate of the new algorithm is favored by a factor of . This result is obtained by expending ‘ball’ to ‘circular cone’ in the step of finding a direction vector.