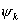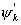A non-uniquely k-colourable graph G is said to be preuniquely k-colourable if the addition of any edge results in a graph G' which either is uniquely k-colourable or has no k-colourings. A k-colouring matrix of a graph G' is determined by the number of vertices in G and two k-colourings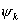 
and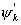 
of G. In this paper properties of k-colouring matrices are given. It is shown how a preuniquely k-colourable graph can be constructed if one of its k-colouring matrices is known.
