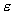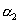A note on the complexity of Swartz's method for calculating the expected delay in non-symmetric cyclic polling systems

Several numerical methods have been proposed in the past for calculating the expected delay in non-symmetric polling systems. However, despite the size of the corresponding numerical problems, very little effort has been devoted to analyzing the overall computational complexity of these methods. As a result, the range of practical applicability of these methods and their relative efficiency are unknown. This note analyzes Swartz's method for computing the expected delay in the discrete time, cyclic polling, exhaustive service system. It shows that the method forms a contraction mapping and, therefore, the number of iterations it requires is logarithmic in the accuracy required. The overall complexity of the method to compute the expected delay for one station is where N is the number of stations, is the accuracy required and depends on the system parameters. The results suggest that, for a wide range of parameters, the approach is the best one known today for computing the expected delay in polling systems, especially if not all N expected delay figures are required. Practical experience shows that the method can be easily used to solve systems with 500 stations or more. Unfortunately, the approach has been used only to analyze a single polling system. It is therefore concluded that it is desirable to apply the approach to other variations of polling systems.