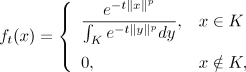Norm-Induced Densities and Testing the Boundedness of a Convex Set

In this paper, we explore properties of a family of probability density functions, called norm–induced densities, defined as 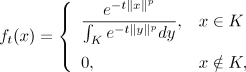$f_t\left(x\right)={\{}_{0\text{,}x\notin K\text{,}}^{\frac{e^{-t{\parallel \parallel x}^p}}{{\int }_K{e}^{-t{\parallel \parallel y}^p}dy}\text{,}x\in K}$ where K is a n–dimensional convex set that contains the origin, parameters t>0 and p>0, and ∥·∥ is any norm. We also develop connections between these densities and geometric properties of K such as diameter, width of the recession cone, and others. Since ft is log–concave only if p≥1, this framework also covers nonlog–concave densities. Moreover, we establish a new set inclusion characterization for convex sets. This leads to a new concentration of measure phenomena for unbounded convex sets. Finally, these properties are used to develop an efficient probabilistic algorithm to test whether a convex set, represented only by membership oracles (a membership oracle for K and a membership oracle for its recession cone), is bounded or not, where the algorithm reports an associated certificate of boundedness or unboundedness.