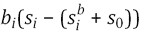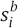Batch scheduling of deteriorating products

In this paper, the authors consider the problem of scheduling N jobs on a single machine, where the jobs are processed in batches and the processing time of each job is a simple linear increasing function depending on job waiting time, which is the time between the start of the processing of the batch to which the job belongs and the start of the processing of the job. Each batch starts from the setup time S. Jobs, which are assigned to the batch, are being prepared for the processing during time S0 < S. After this preparation, they are ready to be processed one by one. The non–negative number bi is associated with job i. The processing time of the i–th job is equal to 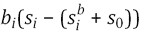$b_i\left(s_i-\left(s_i^b+s_0\right)\right)$ , where 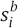$s_i^b$ and si are the starting time of the b–th batch to which the i–th job belongs and the starting time of this job, respectively. The objective is to minimize the completion time of the last job. It is shown that the problem is NP–hard. Then, an O(N) time algorithm solving the problem optimally for the case bi = b is presented, followed by an O(N²) time approximation algorithm with a performance guarantee 2.