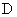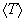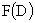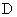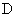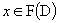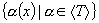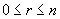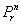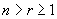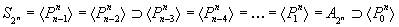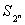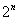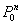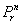A set T of permutations of a finite set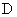 
is said to be transformation complete if the orbits of 
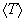, the group generated by T, acting on 
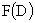, the power set of 
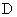, are exactly the set of subsets of 
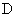having the same cardinality, where the orbit of 
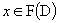is 
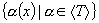. This paper studies the transformation completeness properties of suppressed variable permutation and complementation (SVPC) transformations with act on Boolean variables with domian being 
. An SVPC transformation with r control variables is an identity on the n-cube except on an (n-r)-subcube where the acting is like a variable permutation and complementation (VPC) transformation on n-r variables,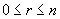 
. Let 
be the set of all SVPC transformations on n variables with r control variables. It is shown that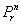 
is transformation complete for 
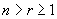. In particular, it is shown that 
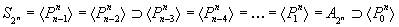. where 
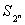and 
are the symmetric group and alternating group of degree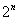 
, respectively. 
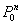, i.e., the VPC transformation group on n variables, is not transformation complete, however, Thus, one control variable is necessary and sufficient to make 
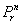transformation complete.
