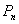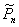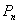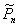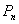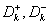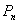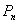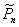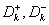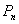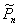This paper considers the Asymmetric Traveling Salesman polytope,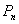 
, defined as the convex hull of the incidence vectors of tours in a complete digraph with n vertices, and its monotonization, 
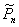. Several classes of valid inequalities for both these polytopes have been introduced in the literature which are not known to define facets of 
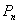or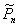 
. The paper describes a general technique which can often be used to prove that a given inequality defines a facet of 
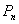. The method is applied to prove that the so-called 
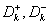C3, comb and C2 inequalities define facets of
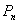, thus solving open problems. As for the monotone polytope, a necessary and sufficient condition for a facet-defining inequality of 
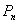to define a facet of 
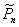as well, as introduced which applies to the 
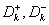C3, comb and C2 inequalities. In addition, a simple procedure for transforming any facet-defining inequality of 
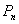into an equivalent one which also defines a facet of 
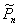, is given.
