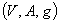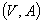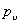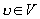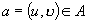| Article ID: | iaor19911678 |
| Country: | United States |
| Volume: | 16 |
| Issue: | 1 |
| Start Page Number: | 208 |
| End Page Number: | 222 |
| Publication Date: | Feb 1991 |
| Journal: | Mathematics of Operations Research |
| Authors: | Schneider Michael H., Schneider Hans |
A weighted directed graph