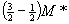The paper considers the problem of scheduling n independent jobs on m identical machines in order to minimize the makespan, the total finishing time. The jobs are available at time zero, but some machines may not be available at time zero. This problem is a generalization of the classical multiprocessor scheduling problem, where all machines are available simultaneously at time zero. The paper first shows that the makespan obtained by applying the longest processing time (LPT) algorithm to the present generalized problem is always within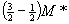 
and the bound is tight. It then provides a modified LPT (MLPT) algorithm and shows that the makespan obtained by MLPT is bounded by
.
