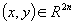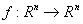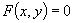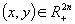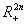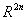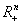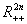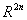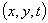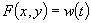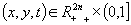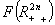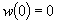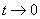| Article ID: | iaor1991657 |
| Country: | United States |
| Volume: | 15 |
| Issue: | 4 |
| Start Page Number: | 662 |
| End Page Number: | 675 |
| Publication Date: | Nov 1990 |
| Journal: | Mathematics of Operations Research |
| Authors: | Kojima Masakazu, Mizuno Shinji, Noma Toshihito |
Defining the mapping