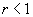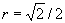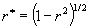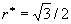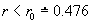In the cookie-cutter game, there is a trapping circle, of radius 1, in which an evader hides. A searcher has a ‘cookie-cutter’, a disk of radius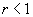 
. If, when he places the cookie-cutter on the trapping circle, the evader is within it, the evader is caught and the searcher wins. Otherwise the evader wins. If 
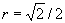, the problem is trivial. The evader should choose a point from the uniform distribution on the outer circumference of the trapping circle, and the searcher a point from the uniform distribution on the circle of radius 
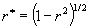concentric to that circle; this choice gives him maximum coverage of the outer circumference. For the case 
, an easy and elegant solution was given by Gale and Glassey in 1974. Both players should go to the center with probability 1/7. The minimizer should go to the outer circumference, and the maximizer to 
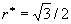, both with probability 6/7. For other r the problem is difficult. This paper proves that there are no solutions based on finitely many radii if 
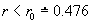, where r 0 solves a cubic equation, finds two-point solutions on 
, where
solves a trigonometric equation, and proves qualitative facts for 
