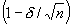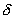An extension of Karmarkar type algorithm to a class of convex separable programming problems with global linear rate of convergence

The authors describe a primal-dual interior point algorithm for a class of convex separable programming problems subject to linear constraints. Each iteration updates a penalty parameter and finds a Newton step associated with the Karush-Kuhn-Tucker system of equations which characterizes a solution of the logarithmic barrier function problem for that parameter. It is shown that the duality gap is reduced at each iteration by a factor of , where is positive and depends on some parameters associated with the objective function.