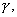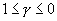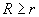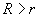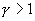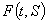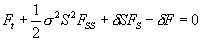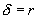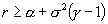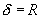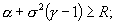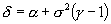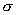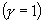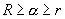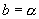The authors construct a stochastic control model of a portfolio in which the investor may invest in stock, call options on the stock, or risk free bonds. He may also borrow funds. The authors assume that the investor is attempting to maximize expected utility of total wealth at expiration of the options where the utility function is given as wealth to the power 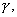
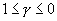 . This includes both the risk averse and risk neutral cases. The authors allow the borrowing interest rate, R, to be distinct from the lending interest rate, r. They make two fundamental assumptions: (i) the investor cannot achieve infinite expected utility of wealth in finite time (‘stable markets’) and (ii) the market will set the option price to minimize the investor's maximal expected utility of wealth, i.e. options are priced using a minimax strategy. The market is stable only when
. This includes both the risk averse and risk neutral cases. The authors allow the borrowing interest rate, R, to be distinct from the lending interest rate, r. They make two fundamental assumptions: (i) the investor cannot achieve infinite expected utility of wealth in finite time (‘stable markets’) and (ii) the market will set the option price to minimize the investor's maximal expected utility of wealth, i.e. options are priced using a minimax strategy. The market is stable only when 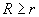 . The authors prove in the case
. The authors prove in the case 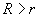 and
and 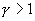 that the minimax (European) call option price,
that the minimax (European) call option price, 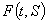 , is given as the solution of the Black-Scholes equation
, is given as the solution of the Black-Scholes equation 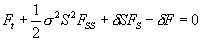 , where
, where 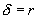 where
where 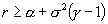 ;
; 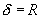 when
when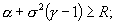 and
and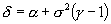 if
if  . The parameter
. The parameter  is the stock return drift and
is the stock return drift and 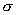 is the stock return diffusion. If
is the stock return diffusion. If  , then the call option price must, by stable markets, always be the Black-Scholes price with rate r. In the risk neutral
, then the call option price must, by stable markets, always be the Black-Scholes price with rate r. In the risk neutral 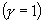 case we must have
case we must have 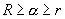 for a stable market and the option price given by the Black-Scholes equation but with
for a stable market and the option price given by the Black-Scholes equation but with 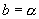 . Explicit solutions are presented and the optimal portfolios and returns are also derived. Comparable results are obtained for American call options which can be exercised at any time up to and including the expiration date. In this case, the option pricing function is shown to be the solution of an obstacle problem.
. Explicit solutions are presented and the optimal portfolios and returns are also derived. Comparable results are obtained for American call options which can be exercised at any time up to and including the expiration date. In this case, the option pricing function is shown to be the solution of an obstacle problem.