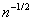Minimum Kolmogorov distance estimates of parameters and parametrized distributions

Minimum Kolmogorov distance estimates of arbitrary parameters are considered. They are shown to be strongly consistent if the parameter space metric is topologically weaker than the metric induced by the Kolmogorov distance of distributions from the statistical model. If the parameter space metric can be locally uniformly upper-bounded by the induced metric then these estimates are shown to be consistent of order . Similar results are proved for minimum Kolmogorov distance estimates of densities from parametrized families where the consistency is considered in the -norm. The presented conditions for the existence, consistency, and consistency of order are much weaker than those established in the literature for estimates with similar properties. It is shown that these assumptions are satisfied e.g. by all location and scale models with parent distributions different from Dirac, and by all standard exponential models.