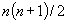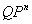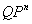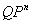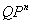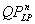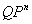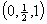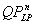| Article ID: | iaor1989573 |
| Country: | Netherlands |
| Volume: | 45 |
| Issue: | 1 |
| Start Page Number: | 139 |
| End Page Number: | 172 |
| Publication Date: | Aug 1989 |
| Journal: | Mathematical Programming |
| Authors: | Padberg Manfred |
The paper studies unconstrained quadratic zero-one programming problems having