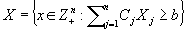| Article ID: | iaor19971032 |
| Country: | Netherlands |
| Volume: | 59 |
| Issue: | 1 |
| Start Page Number: | 57 |
| End Page Number: | 74 |
| Publication Date: | Apr 1995 |
| Journal: | Discrete Applied Mathematics |
| Authors: | Wolsey Laurence A., Pochet Yves |
| Keywords: | optimization |
Three regions arising as surrogates in certain network design problems are the knapsack set