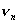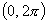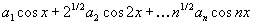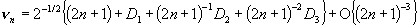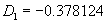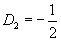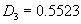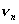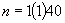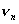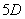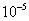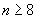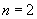| Article ID: | iaor1997302 |
| Country: | United States |
| Volume: | 8 |
| Issue: | 3 |
| Start Page Number: | 299 |
| End Page Number: | 317 |
| Publication Date: | Jul 1995 |
| Journal: | Journal of Applied Mathematics and Stochastic Analysis |
| Authors: | Wilkins J. Ernest, Souter Shantay A. |
| Keywords: | root finding algorithm |
If