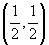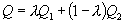| Article ID: | iaor19961859 |
| Country: | Germany |
| Volume: | 42 |
| Issue: | 5 |
| Start Page Number: | 325 |
| End Page Number: | 329 |
| Publication Date: | Sep 1995 |
| Journal: | Metrika |
| Authors: | Obermeyer K., Plachky D. |
It is well-known that the region of risk for testing simple hypotheses is some closed, convex, and