The multi-index transportation problem is an extension of the well-known transportation problem to a problem with multiple subscripted variables 
. Such a problem can have single sums or double sums of the variables as constraints, or triple sums etc., or combinations of different kinds of sums. From this, a great variety of different multi-index problems arise. However, there are some kinds of reduction by which in some cases such a problem can be reduced to another one with less constraints and with less subscripts of its variables. Thus, classes of representatives for all multi-index transportation problems can be found such that any problem is equivalent to such a representative, if necessary by some reductions. This is shown in this paper. Additionally, a suitable way of defining any multi-index transportation problem is given and also an easy way of representing such a problem by a characteristic hypergraph and by a characteristic matrix. Finally, it is demonstrated that the solution of an n-index-problem whose constraints of all kinds of q-fold sums for a fixed value of q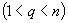 
can be found by solving a problem with only single sums as constraints.
