Using a 1958 result of Lojasiewicz, the authors establish an error bound for analytic systems consisting of equalities and inequalities defined by real analytic functions. In particular, they show that over any bounded region, the distance from any vector x in the region to the solution set of an analytic system is bounded by a residual function, raised to a certain power, evaluated at x. For quadratic systems satisfying certain nonnegativity assumptions, the authors show that this exponent is equal to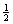 
. They apply the error bounds to the Karush-Kuhn-Tucker system of a variational inequality, the affine variational inequality, the linear and nonlinear complementarity problem, and the 0-1 integer feasibility problem, and obtain new error bound results for these problems. The latter results extend previous work for polynomial systems and explain why a certain square-root term is needed in an error bound for the (monotone) linear complementarity problem.
