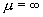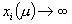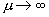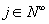| Article ID: | iaor19961386 |
| Country: | Netherlands |
| Volume: | 65 |
| Issue: | 3 |
| Start Page Number: | 347 |
| End Page Number: | 363 |
| Publication Date: | Jul 1994 |
| Journal: | Mathematical Programming (Series A) |
| Authors: | Gler Osman |
The paper studies the limiting behavior of the weighted central paths