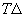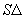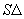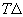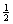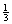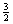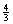| Article ID: | iaor1996615 |
| Country: | Netherlands |
| Volume: | 60 |
| Issue: | 3 |
| Start Page Number: | 273 |
| End Page Number: | 279 |
| Publication Date: | Aug 1992 |
| Journal: | European Journal of Operational Research |
| Authors: | Crama Yves, Spieksma Frits C.R. |
The three-dimensional assignment problem (3DA) is defined as follows. Given are three disjoint