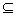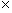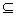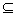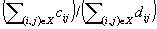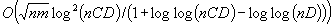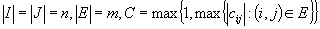| Article ID: | iaor1996316 |
| Country: | Netherlands |
| Volume: | 56 |
| Issue: | 2/3 |
| Start Page Number: | 333 |
| End Page Number: | 343 |
| Publication Date: | Jan 1995 |
| Journal: | Discrete Applied Mathematics |
| Authors: | Matsui Tomomi, Saruwatari Yasufumi, Shigeno Maiko |
| Keywords: | optimization |
In this paper the authors propose a polynomial-time algorithm for