
| Article ID: | iaor1996303 |
| Country: | Netherlands |
| Volume: | 56 |
| Issue: | 1 |
| Start Page Number: | 83 |
| End Page Number: | 86 |
| Publication Date: | Jan 1995 |
| Journal: | Discrete Applied Mathematics |
| Authors: | Gutin G. Blokh, D. |
| Keywords: | graphs, matrices, programming: travelling salesman |
The authors consider the maximizing travelling salesman problem (MTSP) for two special classes of 

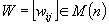
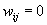
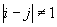
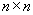
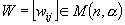
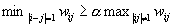

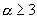
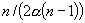
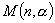
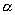
.gif)