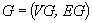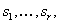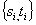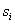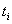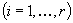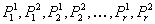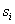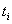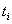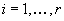Suppose that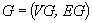 
s a planar graph embedded in the conclusion plane, that I, J, K, O are four of its faces (called holes in G), that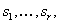 
are vertices of G such that each pair 
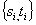belongs to the boundary of some of I, J, K, O, and that the graph 
is eulerian. The paper proves that if the multi(commodity)flow problem in G with unit demands on the values of flows from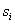 
to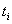 
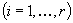has a solution then it has a half-integral solution as well. In other words, there exist paths 
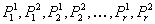in G such that each 
connects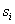 
and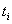 
, and each edge of G is covered at most twice by these paths. (It is known that in case of at most three-holes there exist edge-disjoint paths connecting 
and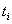 
,
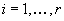, provided that the corresponding multiflow problem has a solution, but this is, in general, false in case of four holes.)
