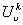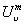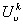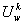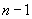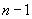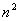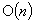| Article ID: | iaor1996276 |
| Country: | Netherlands |
| Volume: | 56 |
| Issue: | 1 |
| Start Page Number: | 61 |
| End Page Number: | 74 |
| Publication Date: | Jan 1995 |
| Journal: | Discrete Applied Mathematics |
| Authors: | Norris N. |
| Keywords: | fuzzy sets |
Vertex- and edge-labeled digraphs have been used to model computer networks, and the universal covers of such graphs to describe what a processor in an anonymous network ‘knows’ about the network. If