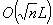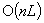In a recent paper, Shaw and Goldfarb show that a version of the standard form projective algorithm can achieve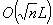 
step complexity, as opposed to the 
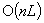step complexity originally demonstrated for the algorithm. The analysis of Shaw and Goldfarb shows that the algorithm, using a constant, fixed steplength, approximately follows the central trajectory. In this paper it is shown that simple modifications of the projective algorithm obtain the same complexity improvement, while permitting a linesearch of the potential function on each step. An essential component is the addition of a single constraint, motivated by Shaw and Goldfarb's analysis, which makes the standard form algorithm strictly monotone in the true objective.
