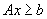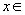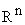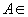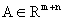| Article ID: | iaor19951877 |
| Country: | Slovakia |
| Volume: | 1 |
| Issue: | 4 |
| Start Page Number: | 247 |
| End Page Number: | 260 |
| Publication Date: | Oct 1992 |
| Journal: | Czechoslovak Journal for Operations Research |
| Authors: | Falk James E., Fagan James T. |
In this paper the authors describe a new algorithm for solving a linear programming problem of the form: max