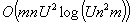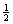The problem of integer programming in bounded variables, over constraints with no more than two variables in each constraint is NP-complete, even when all variables are binary. This paper deals with integer linear minimization problems in n variables subject to m linear constraints with at most two variables per inequality, and with all variables bounded between 0 and U. For such systems, a 2-approximation algorithm is presented that runs in time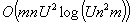 
, so it is polynomial in the input size if the upper bound U is polynomially bounded. The algorithm works by finding first a super-optimal feasible solution that consists of integer multiples of 
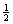. That solution gives a tight bound on the value of the minimum. It furthermore has an identifiable subset of integer components that retain their value in an integer optimal solution of the problem. These properties are a generalization of the properties of the vertex cover problem. The algorithm described is, in particular, a 2-approximation algorithm for the problem of minimizing the total weight of true variables, among all truth assignments to the 2-satisfiability problem.
