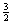Local convergence analysis of tensor methods for nonlinear equations

Tensor methods for nonlinear equations base each iteration upon a standard linear model, augmented by a low rank quadratic term that is selected in such a way that the mode is efficient to form, store, and solve. These methods have been shown to be very efficient and robust computationally, especially on problems where the Jacobian matrix at the root has a small rank deficiency. This paper analyzes the local convergence properties of two versions of tensor methods, on problems where the Jacobian matrix at the root has a null space of rank one. Both methods augment the standard linear model by a rank one quadratic term. The authors show under mild conditions that the sequence of iterates generated by the tensor method based upon an ‘ideal’ tensor model converges locally and two-step Q-superlinearly to the solution with Q-order , and that the sequence of iterates generated by the tensor method based upon a practical tensor model converges locally and three-step Q-superlinearly to the solution with Q-order . In the same situation, it is known that standard methods converge linearly with constant converging to . Hence, tensor methods have theoretical advantages over standard methods. The present analysis also confirms that tensor methods converge at least quadratically on problems where the Jacobian matrix at the root is nonsingular.