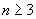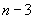| Article ID: | iaor19951525 |
| Country: | Netherlands |
| Volume: | 43 |
| Issue: | 1 |
| Start Page Number: | 63 |
| End Page Number: | 74 |
| Publication Date: | May 1993 |
| Journal: | Discrete Applied Mathematics |
| Authors: | Sierksma Gerard |
The vertices of the skeleton of the symmetric Traveling Salesman Polytope are the characteristic vectors corresponding to the Hamiltonian tours in the complete graph