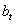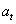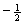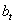| Article ID: | iaor19951171 |
| Country: | Netherlands |
| Volume: | 50 |
| Issue: | 2 |
| Start Page Number: | 331 |
| End Page Number: | 347 |
| Publication Date: | Apr 1994 |
| Journal: | Stochastic Processes and Their Applications |
| Authors: | Pruscha Helmut |
The paper considers a multivariate point process with a parametric intensity process which splits into a stochastic factor