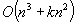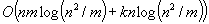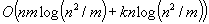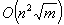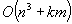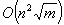| Article ID: | iaor19951108 |
| Country: | United States |
| Volume: | 11 |
| Issue: | 3 |
| Start Page Number: | 278 |
| End Page Number: | 290 |
| Publication Date: | May 1994 |
| Journal: | Algorithmica |
| Authors: | Gusfield D., Tardos E. |
Gallo et al recently examined the problem of computing on-line a sequence of