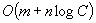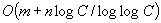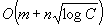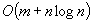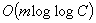| Article ID: | iaor1995714 |
| Country: | United States |
| Volume: | 37 |
| Issue: | 2 |
| Start Page Number: | 213 |
| End Page Number: | 223 |
| Publication Date: | Apr 1990 |
| Journal: | Journal of the Association for Computing Machinery |
| Authors: | Tarjan Robert E., Orlin James B., Ahuja Ravindra K., Mehlhorn Kurt |
Efficient implementations of Dijkstra's shortest path algorithm are investigated. A new data structure, called the