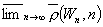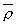A preference foundation for log mean-variance criteria in portfolio choice problems

The appropriate criterion for evaluating, and hence also for properly constructing, investment portfolios whose performance is governed by an infinite sequence of stochastic returns has long been a subject of controversy and fascination. A criterion based on the expected logarithm of one-period return is known to lead to exponential growth with the greatest exponent, almost surely; and hence this criterion is frequently proposed. A refinement has been to include the variance of the logarithm of return as well, but this has had no substantial theoretical justification. This paper shows that log mean-variance criteria follow naturally from elementary assumptions on an individual's preference relation for deterministic wealth sequences. As a first and fundamental step, it is shown that if a preference relation involves only the tail of a sequence, then that relation can be extended to stochastic wealth sequences by almost sure equality. It is not necessary to introduce a von Neumann-Morgenstern utility function or the associated axioms. It is then shown that if tail preferences can be described by a ‘simple’ utility function, one that is of the form where is wealth at period n, this utility must under suitable conditions be a function of the expected logarithm of return, independent of the functional form of . Finally, ‘compound’ utility functions are introduced; and they are shown under suitable conditions to be functions of the expected value and variance of the logarithm of one-period return, again independently of the specific form of the underlying function. The infinite repetitions of the dynamic process essentially ‘hammer’ all utility functions into a log mean-variance form.