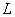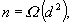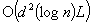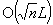A randomized scheme for speeding up algorithms for linear and convex programming problems with high constraints-to-variables ratio

The authors extend Clarkson's randomized algorithm for linear programming to a general scheme for solving convex optimization problems. The scheme can be used to speed up existing algorithms on problems which have many more constraints than variables. In particular, the authors give a randomized algorithm for solving convex quadratic and linear programs, which uses the scheme together with a variant of Karmarkar's interior point method. For problems with n constraints, d variables, and input length , if the expected total number of major Karmarkar's iterations is , compared to the best known deterministic bound of . The authors also present several other results which follow from the general scheme.