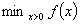To deal with the optimization problem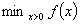 
, the authors propose a Gauss-Seidel type iterative approach where variables are modified sequentially one at a time (GSNA algorithm) or by blocks (BGSNA algorithm). Relying on both the Newton approach and an Armijo rule, an inaccurate line search is performed at each step to determine a step size insuring global convergence. Both robustness (global convergence) and efficiency (rate of local convergence) are analyzed under minimal hypotheses even weaker than those often required to prove the convergence of Gauss-Seidel methods. These procedures are applied to spatial price equilibrium problems, and the numerical results indicate that they are competitive with MINOS.
