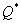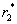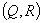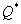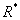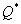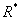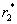For a variety of reasons, many firms purchase a given inventory item from two or more suppliers. For a situation where two competing suppliers (supplier-1 and supplier-2) offer different prices, quality levels and lead-time performance, the authors present a decision model and solution procedure for obtaining a lowest-cost ordering policy; this policy prescribes R* (the optimal reorder point),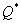 
(the optimal lot size for each order), and 
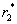(the optimal proportion that should be ordered from supplier-2). A continuous-review inventory system with complete backordering is assumed. The present decision model has two parts. The first part uses a minor modification of the classical Hadley-Whitin single-supplier continuous review 
model to determine the optimal ordering policy (i.e., 
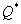and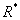 
) when only supplier-1 (or only supplier-2) is used. In the second part, a new two-supplier extension of the Hadley-Whitin-type cost model developed here is used to determine the optimal policy (i.e., 
, 
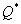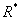and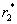 
) when both suppliers have to be used. From the three optimal policies (one each for ‘using supplier-1 only’, ‘using supplier-2 only’, and ‘using both suppliers’), the lowest-cost policy is identified. The present numerical solutions show that whether one or both of the suppliers should be used and the optimal order-split proportion depends on the particular combination of the inventory item's many cost and demand parameters (e.g., shortage cost per unit, holding cost per unit per year, standard deviation of lead time, etc.). The procedure can easily identify the optimal policy for any given combination of those parameters. The present numerical sensitivity analyses indicate that the coordination of two suppliers is beneficial in a wide variety of situations where the various inventory parameters have intermediate (i.e., neither very high nor very low) values.
