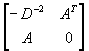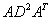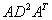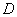| Article ID: | iaor19941986 |
| Country: | Netherlands |
| Volume: | 58 |
| Issue: | 1 |
| Start Page Number: | 1 |
| End Page Number: | 32 |
| Publication Date: | Jan 1993 |
| Journal: | Mathematical Programming (Series A) |
| Authors: | Vanderbei Robert J., Carpenter Tamra J. |
| Keywords: | programming: linear |
The authors present a unified framework for solving linear and convex quadratic programs via interior point methods. At each iteration, this method solves an indefinite system whose matrix is