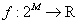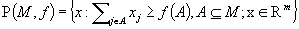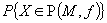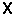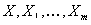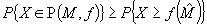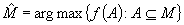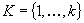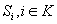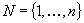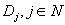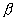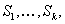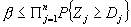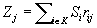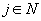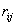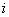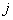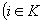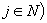For 
and a supermodular set function 
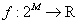, define the polymatroid 
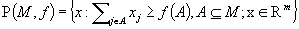. The authors develop a bound for the probability 
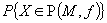, where 
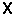is a random m-vector. In particular they show that if 
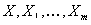, are independent and identically distributed nonnegative random variables with new better than used (NBU) distribution function, then 
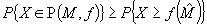, where 
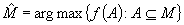. á(NBU) distribution function, then >F100<P >F003<A>F004<X >F003<. >F109<p>F000<(>F100<màAF02,àAF12f >F000<)>F003<S e >F100<P >F003<A>F100<X >F003<e >F100<f >F000<(>F100 H08W08<M>$-55<àI>F000 H08W09.5J102<ˆàR>$29 F100 H08W08< >F000<)>F003<S>F100<àAF02, >F000<where >F100 H08W08<M>$-55<àI>F000 H08W09.5J102<ˆàR>$29 F100 H08W08< >F000<= argàAF12max>F003<A>F100<f >F000<(>F100<A>F000<):àAF12>F100<A >F001<Y >F100<M >F003<S>F100<. The authors apply this result to transportation problems with random supply and/or demand. Suppose they have a set 
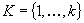of k supply nodes with a random supply 
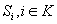and a set 
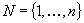of n demand nodes with a random demand 
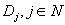. Let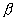 
be the probability that the random demand can be met by the random supply. If the demand and supply are mutually independent, 
are independent, and 
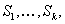are independent and have NBU distribution function, then 
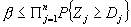, where 
, 
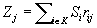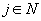and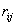 
takes the value one if node 
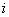can supply the demand node 
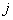and zero otherwise 
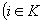and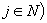 
.
