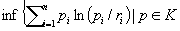| Article ID: | iaor19941982 |
| Country: | Germany |
| Volume: | 37 |
| Start Page Number: | 285 |
| End Page Number: | 301 |
| Publication Date: | Feb 1993 |
| Journal: | Mathematical Methods of Operations Research (Heidelberg) |
| Authors: | Kortanek K.O. |
| Keywords: | semi-infinite programming |
The equivalence of multinomial maximum likelihood and the isotonic projection problem: