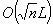The authors present an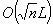 
-iteration homogeneous and self-dual linear programming (LP) algorithm. The algorithm possesses the following features: It solves the linear programming problem without any regularity assumption concerning the existence of optimal, feasible, or interior feasible solutions. It can start at any positive primal-dual pair, feasible or infeasible, near the central ray of the positive orthant (cone), and it does not use any big M penalty parameter or lower bound. Each iteration solves a system of linear equations whose dimension is almost the same as that solved in the standard (primal-dual) interior-point algorithms. If the LP problem has a solution, the algorithm generates a sequence that approaches feasibility and optimality simultaneously; if the problem is infeasible or unbounded, the algorithm will correctly detect infeasibility for at least one of the primal and dual problems.
