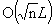Recently, Ye, Tapia and Zhang demonstrated that Mizuno-Todd-Ye's predictor-corrector interior-point algorithm for linear programming maintains the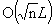 
-iteration complexity while exhibiting superlinear convergence of the duality gap to zero under the assumption that the iteration sequence converges, and quadratic convergence of the duality gap to zero under the assumption of nondegeneracy. In this paper the authors establish the quadratic convergence result without any assumption concerning the convergence of the iteration sequence or nondegeneracy. This surprising result, to the present knowledge, is the first instance of a demonstration of polynomiality and superlinear (or quadratic) convergence for an interior-point algorithm which does not assume the convergence of the iteration sequence or non-degeneracy.
