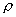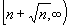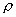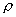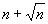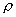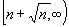| Article ID: | iaor19941928 |
| Country: | Netherlands |
| Volume: | 58 |
| Issue: | 2 |
| Start Page Number: | 243 |
| End Page Number: | 255 |
| Publication Date: | Feb 1993 |
| Journal: | Mathematical Programming (Series A) |
| Authors: | Kortanek K.O., Huang S., Ye Y., Kaliski J. |
| Keywords: | duality |
This paper is concerned with selection of the