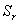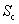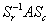Hierarchical decomposition of symmetric discrete systems by matroid and group theories

An algebraic method is proposed for the hierarchical decomposition of large-scale group-symmetric discrete systems into partially ordered subsystems. It aims at extracting ‘substructures’ and ‘hierarchy’ for such systems as electrical networks and truss structures. The mathematical problem considered is: given a parametrized family of group invariant ‘structured’ matrices A, the paper finds two constant ( =parameter-independent) nonsingular matrices and such that takes a (common) block-triangular form. The proposed method combines two different decomposition principles developed independently in matroid theory and in group representation theory. The one is the decomposition principle for submodular functions, which has led to the Dulmage-Mendelsohn decomposition and further to the combinatorial canonical form of layered mixture matrices. The other is the full reducibility of group representations, which yields the block-diagonal decomposition of group invariant matrices. The optimality of the proposed method is also discussed.